With qubits being the standard for quantum computation everywhere, people often don’t know that there are many other options available if you are willing to do a bit of digging.

One of those that I wish to discuss today is CV (Continuous-Variable) Quantum States. Specifically, we will see how they are different from DV (Discrete-Variable) Quantum States, how these states are represented, and what advantages they have compared to the regular qubits we know and love.

Let’s dive in! 🔎

Discrete-Variable Quantum States

Let’s start by explaining what everyone should already be familiar with — quantum states of the following form: |ψ⟩ = α |0⟩ + β |1⟩

Here, |ψ⟩ is our qubit, while α and β are complex number coefficients. Quantum information is represented simply by transforming these coefficients through various operations. It’s all about working with probabilities by manipulating them to get the results we want!

This approach is called DV Quantum Computation, the most common type of quantum computation.

However, just because it is the most common method does not mean it is the best method. If you think about it, the fact that engineers decided to limit photons, electrons, and other forms of matter to two levels seems quite odd don’t you think?

For starters, these forms of matter do not naturally have two energy levels. We actively have to go out of our way to isolate their energy levels to be able to use them as qubits.

Moreover, although measurement results are binary, values encoded in the coefficients (α and β) are not! Imagine how much data we may be losing due to this transformation. I mean, it’s not certain how analogous DV quantum computation is to classical, digital computation.

But if the way we understand quantum states today is simply an engineered version of reality, how do we accurately represent natural quantum states?

Continuous-Variable Quantum States

Instead of qubits, how about we try representing states in the following form:

This is how quantum mechanics was originally formulated. The x could be a parameter, such as the position of a particle among other things, while our physical quantities can take continuous values instead of binary values.

As you might guess, this method is called CV Quantum Computation, where the smallest unit of information is referred to as a mode or qumode.

Instead of manipulating the two coefficients α and β, we manipulate the wave function ψ(x).

CV quantum states can be equivalently written as:

where n is an integer representing things such as photon numbers in an optical system. Why is this interesting, you may ask?

Well, the Hilbert Space of DV quantum computing is quite literally a subset of CV quantum computing because it includes both discrete and continuous representations of states.

This means that we can think of quantum states and measurements using either continuous parameters x or discrete values n, allowing us to take advantage of both approaches!

Just to be clear, when I say “discrete values” I don’t mean binary values! The difference is quite simple really —while binary values refer specifically to a two-state system such as the |0⟩ and |1⟩ states in quantum computing, discrete values can refer to any quantized, countable number of states, like |n⟩, which could be any integer (not just |0⟩ or |1⟩).

The complementary relationship between DV and CV quantum computing is somewhat similar to the wave-particle duality. In an optical system, for example, we can describe and measure quantum states using either the amplitude of their electric fields x (wave picture) or their photon count n (particle picture).

They both represent the same system, it’s just that they are two completely different ways of looking at the system!

Advantages of Optical Hardware

I’ve mentioned optical systems twice so far in this article (now thrice).

You as the reader may have noticed a great amount of emphasis on optical-based quantum computation on my part, even though the concept we are talking about (CV Quantum States, just in case you forgot) can be applied more generally to other types of quantum hardware as well.

For our discussion, however, we will continue to stick to Optical Systems as they are quite practical for implementing CV Quantum States. Here are some reasons why.

Optical systems can be implemented at room temperature at atmospheric pressure. This means that, unlike superconducting computing methods, you don’t need to cool the system down to millikelvin-level temperatures.

Moreover, optical systems can easily be integrated into existing telecommunication networks, making them very promising candidates when considering applications such as quantum communications and cryptography.

However, classical optical computers (including analog ones!) suffer a severe limitation; reliable copying of analog information, as well as error correction, is very difficult if even possible at all — these are the problems that CV Optical Quantum Computation aims to solve.

Copying Information

I want to start by discussing the problem of copying information, which can be translated to the problem of transferring quantum states reliably. From an algorithmic perspective, it’s quite a trivial problem in quantum computing!

Now, Quantum Computing is governed by the laws of Quantum Mechanics, which states that you cannot simply make an exact copy of an unknown quantum state. This is called the no-cloning theorem.

This means that we can only “copy” classical states. So with this bit of information, how can we devise an algorithm that can copy the state of one qumode to another?

Enter Quantum Teleportation! This badly named algorithm doesn’t physically transfer matter from one place to another but rather uses classical bits that store quantum states so they can be used later on. You can read more about it here.

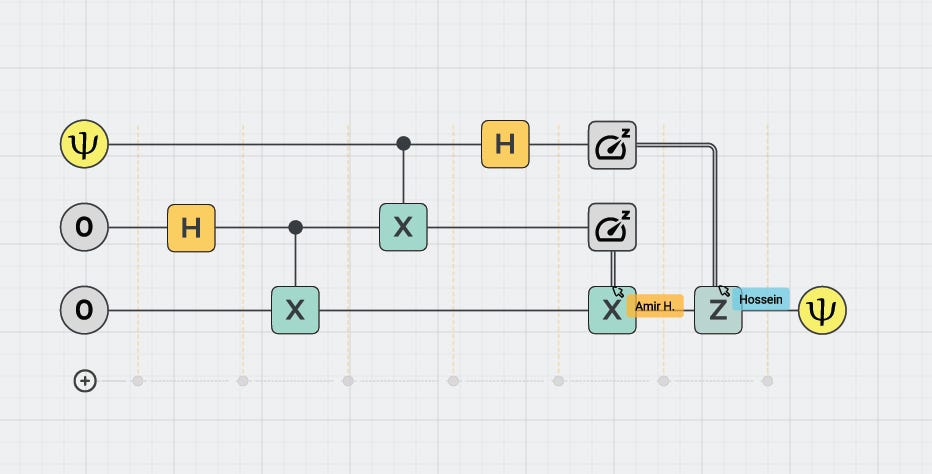
Alright, so that’s one problem out of the way. Now, how about Error Correction?

There are currently no error correction methods that work as well as we need them to (having thousands of fault-tolerant qubits). At least, not without the need to have a massive infrastructure that would introduce major operational challenges to the problem.

What I find quite ironic is that, after all this talk of using qumodes and how they can represent quantum information more naturally, common methods for error correction in CV Quantum Computing Systems are done with qubits 😂

Error Correction — GKP Qubits

Remember how I mentioned that CV Quantum States can be either discrete or continuous? Well, the Gottesman-Kitaev-Preskill (GKP) Qubit is a discrete qubit designed to be embedded within a continuous system.

It cleverly “locks” certain important values into a grid, where we can easily tell if something goes wrong, using a system where the quantum information is encoded into wavefunctions that look like a series of spikes at specific positions.

Let’s imagine drawing a grid of points on a piece of paper, representing the wavefunctions. Each point represents a possible value of the qubit. If some noise bumps a value away from one of these points, the grid helps us know where it should have been, so we can “correct” it back to the right place — that’s the core idea.

They are positioned in such a way that even if the wave function gets slightly disturbed (by noise or errors), we can still figure out where the original information was supposed to be!

What’s even more interesting is that the wavefunctions are placed into a lattice structure, designed to be resilient against small errors, helping keep information intact even in noisy environments.

Welp folks, that’s the end of Part 1! 

I wanted to split this topic into two parts so that you wouldn’t be overwhelmed.

In Part 2 of this article, we are going to dive into the specifics of how CV Quantum States can be realized on Optical Hardware, what problems we are currently facing with these systems, and how we aim to resolve them in the upcoming years.